Let’s solve an easy algorithmic task with the most convoluted (pun intended) approach possible. Why? Because we can.

Background

Consider the canonical algorithmic task of sorting an array of numbers. Of course, there are a plethora of existing, well-analyzed routines that accomplish such a task, such as merge sort, bubble sort, insertion sort, and so on.

An interesting and unanswered problem arises in authentically mimicking this functionality strictly using Convolutional Neural Networks. On the one hand, we know of course from the universal approximation theorem that deep nets have the theoretical capacity to approximate any arbitrary function. However, it is an open question in the field whether CNNs are Turing Complete. Practically, for our purposes, this implies that it is uncertain if CNNs can reliably execute a given sorting algorithm.

In any case, there doesn’t seem to be any prior literature in the field regarding CNN-sorting, and as such, the proposed task poses an interesting and open-ended challenge.

Formal Problem Definition

Before diving into the proposed solutions, we outline a few key assumptions regarding the form of our input array. In general, arrays of numbers need not fit the following criteria, but for the purposes of this analysis, we will assume them for convenience. We rank the assumptions in descending order from strongest to weakest, outline the implications they have on our two proposed algorithms, and provide quick sketches of extensions that generalize our solutions to such cases:

  1. The arrays are of fixed even length.
    • This is actually only a requirement for Proposal A, as the Seq2Seq nature of Proposal B allows for variable input length, barring massively-sized arrays that can’t fit in memory. In a sense, this requirement is also fairly “soft” as far as Proposal A is concerned. That is, we propose an architecture here specifically for 32-length inputs, but the underlying progression of filter properties across layers follows a strict pattern that is easily extrapolated to longer length inputs. However, our Proposal A architecture is not as amenable to odd-length inputs.
  2. The numbers are non-negative.
    • This is more or less a trivial requirement, specifically for Proposal B. In brief, the Encoder-Decoder structure of that Seq2Seq model relies on non-negative indices to embed the input data. However, this restriction is easily evaded if the input is mapped to a positive domain, fed into the model, and the output is constant-shifted back into the original domain. Thus, we don’t really need the input numbers to be non-negative.
  3. The numbers are integers.
    • This is actually not prohibitive at all for either proposed Solution, but we chose to restrict the input array datatype to integers to focus on nailing the underlying mechanics of these algorithms (much in same way introductory Computer Science courses avoid non-integers when introducing the classic sorting algorithm).

With these assumptions out of the way, we will now introduce our two proposed solutions, the first of which is a Merge Sort-flavored implementation, and the second a neural machine translation architecture that has been repurposed for numerical sequences and reimplemented without the need for Recurrent Neural Networks.

Proposal A: Merge Sort Approach

Inspiration

Traditionally, Merge Sort is an efficient, general-purpose, and comparison-based sorting algorithm following the Divide-and-Conquer paradigm. Its recursive nature divides the input array into two halves, calls itself on the two halves, and then merges the two sorted halves.

The key insight that we’ve drawn from this routine is from the re-assembling portion of the algorithm. That is, one can imagine that the input array to any given neural network is already in the form of a collection of singletons (i.e. equivalent to the fully-divided stage of Merge Sort). Thus, all that remains is a method for learning how to combine these singleton elements in a Merge Sort-like fashion.

The analogy between Merge Sort and even-filtered 1D Convolutions is almost a natural one, and I decided to first implement this approach.

Architecture and Implementation

The proposed and implemented architecture attempts to do precisely that. We assume here an input array of length 32. The (stupid simple) architecture is then as follows:

  • 1D Convolution: 32 filters of width 2 and stride 1 with ReLU activation
  • 1D Convolution: 32 filters of width 2 and stride 1 with ReLU activation
  • Convolution: 32 filters of width 4 and stride 1 with ReLU activation
  • Convolution: 32 filters of width 4 and stride 1 with ReLU activation
  • 1D Convolution: 64 filters of width 8 and stride 1 with ReLU activation
  • 1D Convolution: 64 filters of width 8 and stride 1 with ReLU activation
  • 1D Convolution: 64 filters of width 16 and stride 1 with ReLU activation
  • 1D Convolution: 64 filters of width 16 and stride 1 with ReLU activation
  • 1D Convolution: 128 filters of width 32 and stride 1 with ReLU activation
  • 1D Convolution: 128 filters of width 32 and stride 1 with ReLU activation
  • Fully Connected Layer: 4096-by-32 weight mapping

The padding at each layer is calculated to ensure that the output of each layer is of the same dimension as the input to each layer.

Notably, observe that we have chosen to incorporate even-numbered filters in our model, unlike the majority of CNN architectures (at least for vision tasks). The intuition here is that in conventional Merge Sort for a 32-length input, the algorithm would only ever consider even-length subproblems (barring the initial merging of singletons). As such, to remain authentic to the Merge Sort flavor, we elect to only choose even-length filters.

Similar to most CNN architectures, we also increase the number of filters at each layer. Of course, this choice follows the conventional wisdom that the larger the number of filters, the larger the number of abstractions that our network is able to extract from the raw data.

We do not incorporate any Max Pooling layers, as from our experiments we do not see any notable benefit from incorporating Max Pooling to downsample (offset by an increased number of filters). Indeed, in many cases the model overfits after incorporating Max Pooling. This is likely because the input data is so low-dimensional to begin with.

We also do not incorporate any Dropout or any other regularizers, as based on our experiments, our lightweight model does not tend to overfit the data; validation loss consistently hovers right around training loss with our implementation.

Critically, our model returns an array of floats as output. As a means of post-processing, we refine this output by rounding each float value to the nearest value of the original input array.

We train the model on a training set of 100,000 randomly generated NumPy arrays, and a validation set of 20,000 similarly generated arrays.

To view the Keras implementation, please refer to the following link.

Example Sorted Output
Fig. 1 - Example Sorted Output

ConvMerge: Metrics and Results

To measure our model performance, we needed to define a custom loss-function. Of course, the first thing that comes to mind is some sort of edit distance; however, a traditional edit distance metric doesn’t account for how “close” a predicted value in the array is to the ground truth value.

Another reasonable approach is to consider some form of a regression loss. The obvious candidate is MSE; but since our output values are arrays and not individual numbers, a slight modification is needed.

Ultimately, we define a custom loss function we dub “Mean Squared Euclidean Error”. As the name suggests, it is simply the mean of the Euclidean Distance between the ground truth and predicted arrays:

\[MSEE = \frac{1}{N} \sum_{i=1}^{N} \sum_{j = 1}^M (\hat{y_{ij}} - {y_{ij}})\]

Here $N$ is the total number of samples and $M$ is the input/output dimension (i.e. 32).

We are able to obtain a MSEE validation loss of 3.398 after training for ~20 minutes on a K80 GPU (p2.xlarge instance), with Wandb logging to monitor performance.

Proposal B: Conv-Seq2Seq-Sort

Inspiration

As a less conventional, but more interesting approach, we also implement a CNN that replaces the role of a RNN in a Seq2Seq machine translation architecture.

The inspiration for this approach is simple, but bold. Instead of taking a structured algorithm like Merge Sort and attempting to “encode” that behavior into a ConvNet, we instead treat the sorting problem as a pure translation problem, from the “language” of unsorted arrays to the “language” of sorted arrays.

Originally, this approach was inspired by Yoon Kim’s Convolutional Neural Networks for Sentence Classification paper, and this seeded the idea that it might be possible to leverage CNNs to perform translation.

Ultimately, we write a PyTorch implementation of the Convolutional Sequence to Sequence Learning paper. The implementation is modified to handle the lower-dimensional embeddings of numbers (as opposed to larger-dimension pretrained word embeddings like GloVe), and to account for the choice of a regression-flavored loss function of arrays of numbers (as opposed to a combinatorially complex CrossEntropy-type loss function acting on the space of arrays of vectors).

Architecture and Implementation

An overview of the model, from the original paper, is shown below:

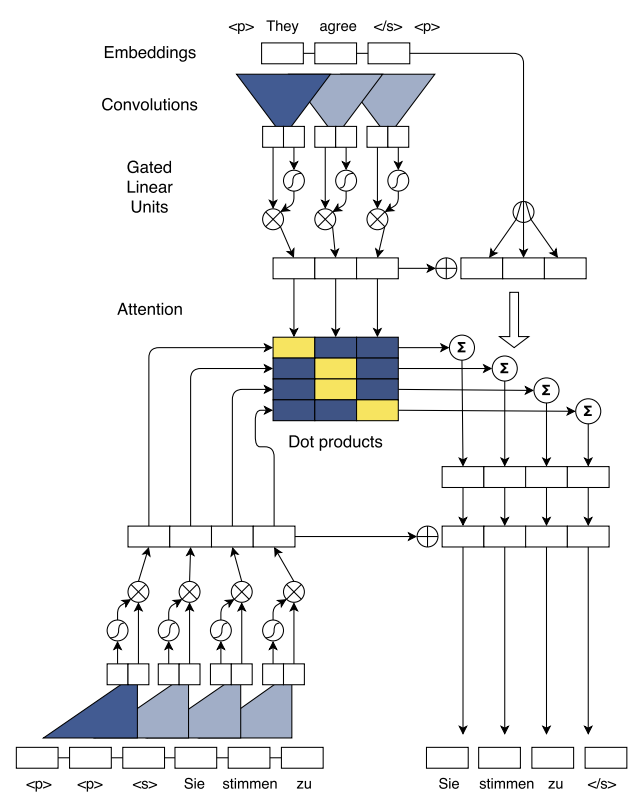
Convolutional Sequence to Sequence Learning Architecture
Fig. 2 - Convolutional Sequence to Sequence Learning Architecture

There are a lot of moving parts here, but the core ideas to keep track of are the Encoder and Decoder, as well as the convolutional blocks that comprise each subarchitecture.

Concretely, the scheme in the Encoder calculates two context vectors for each token in the input array. Without diving too much into the details, the Encoder essentially embeds each input token (number) into a lower-dimensional vector space, and then passes this vector through a few convolutional blocks, sums, and residual connections, before being mapped back into the original input space.

We focus here primarily on the concept of the convolutional block. Each block is a 2D convolution, followed by GLU activation, and then a residual connection. There is dropout at the beginning of each convolutional layer. Of course, padding is included to preserve fixed dimensions. Below is an illustration of this architecture:

Convolutional Block Architecture
Fig. 3 - Convolutional Block Architecture

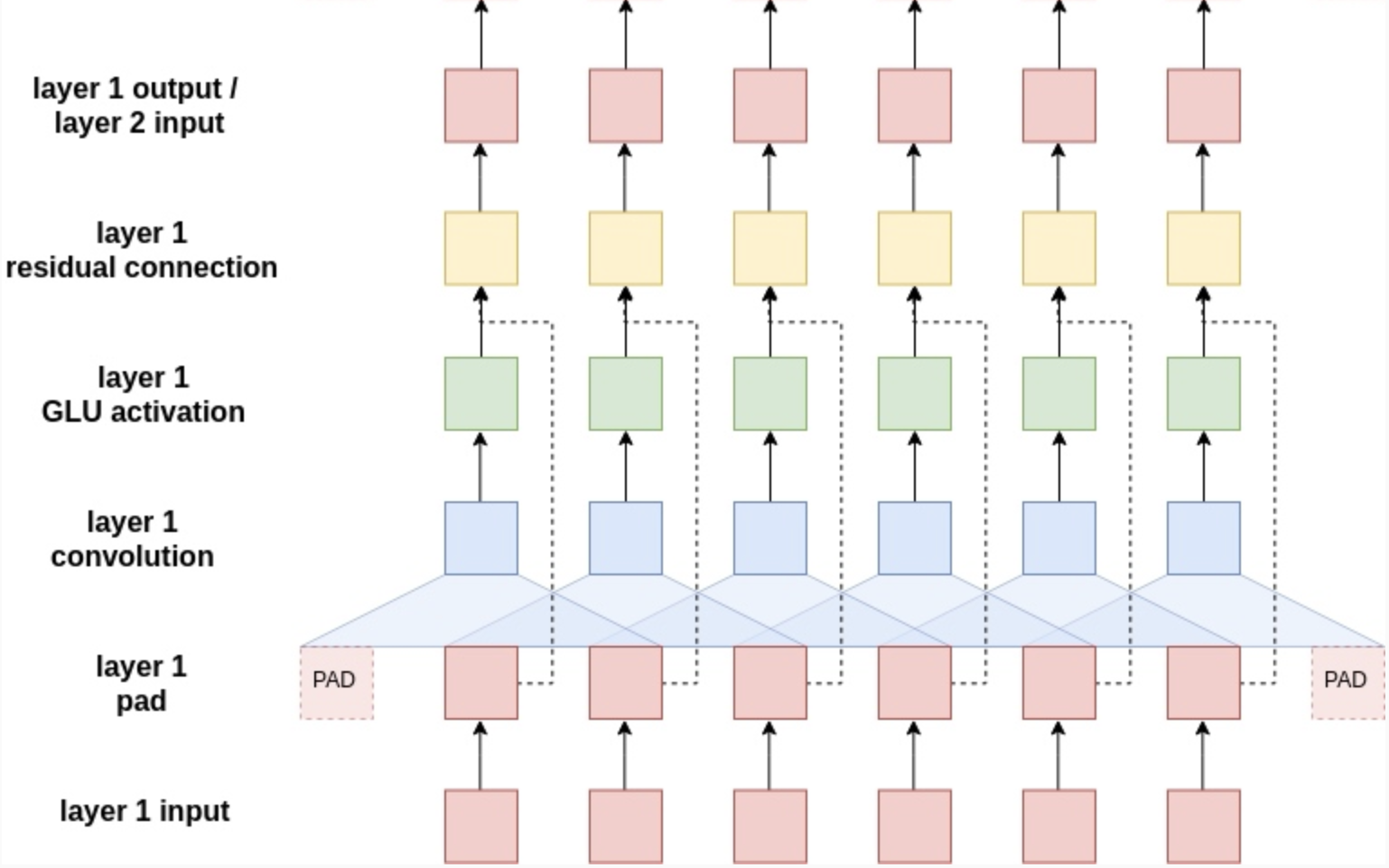
In our implementation of the Encoder and Decoder, we include 13 stacked convolutional blocks each.

As is standard in neural machine translation, the context vectors of the Encoder are fed alongside past tokens in the target space to the Decoder, which predicts the next token. We do not use teacher forcing due to its adverse effect on model generalizability.

As is not standard in neural machine translation, the Decoder does not output a distribution amongst the categories of the target vocabulary – it predicts single numbers. This is what enables us to use the same MSEE loss as defined in section ConvMerge: Metrics and Results. This is a major departure from standard NLP techniques, but we feel it is the appropriate approach for the sorting task at hand, as we feel it is more intuitive and interpretable to have a numbers-to-numbers loss function rather than a discrete loss function acting in the space of vector embeddings. Put bluntly, there is no need to vectorize numbers in order to measure similarity, as there is for the discrete space of language.

Metrics and Results

Critically, we attempt to model 128-length arrays. This choice of a more challenging problem was driven by the fact that this model is much more expressive, with much more parameters, than the Merge Sort model.

We obtain a best model with a validation loss of 3.649.

To view the model results, please refer to the implementation for a pre-trained model and testing code.

Further Exploration

On a first cut, we would like to further address the restrictions proposed in the Formal Problem Definition. All of these are indeed solvable, (if not already accounted for) in particular by Proposal B.

Now as far as Proposal B goes, we believe there is a lot of remaining room for exploration, especially on the front of sorting non-integer data. In particular, our method of using Seq2Seq with a regression-flavored loss function is not well tested nor understood in the field. With that being said, a pure word-embedding approach is unlikely to perform well, given the fact that the majority, if not all, the datasets that canonical word embeddings (GloVe, Word2Vec, etc.) are derived from contain extremely sparse non-integer data within the vocabulary.

Recent research has considered the task of explicitly learning numeral embeddings. It would be a very natural next step to incorporate these well-learned pre-trained embeddings as part of our Seq2Seq model, and revert back to the standard NLP procedure of using Categorical Cross Entropy as a our loss function, instead of our proposed MSEE loss here.